Spektralprofil einer rotierenden Gasscheibe
Ich möchte gerne die mathematischen Grundlagen vorstellen, die die gemessenen Rotationsgeschwindigkeiten beschreiben, die man misst, wenn man den Spektrographen-Spalt über eine rotierende Gasscheibe legt.
Das Modell ist dabei recht einfach – man geht von einer rotierenden Gasscheibe aus, die eine Keplersche Rotation aufweist:
Mit zunehmender Entfernung r vom Zentrum der Scheibe nimmt die Geschwindigkeit ab. Die Rotationsgeschwindigkeit ist ein Vektor, der tangential ausgerichtet ist, d.h. in der Scheibenebene liegt. Für die gemessene Rotationsgeschwindigkeit ist nun die Lage der Scheibenebene, relativ zur Beobachtungsrichtung, wichtig – diese bestimmt die radiale Komponente des Geschwindigkeitsvektors, und damit die messbare Rotationsgeschwindigkeit. In dem Modell wird die Orientierung Scheibenebene-Beobachter durch die Inklination i beschrieben. Ist die Inklination 0° blickt man frontal auf die Scheibenebene, bei i = 90°betrachtet man die Scheibe „edge on“, und man misst die maximalen Radialkomponenten.
Für die weitere Betrachtung nutzt man zwei Koordinatensysteme – zum einen das in der gekippten Scheibenebene, und zum einen das in der Projektionsebene, die senkrecht zur Beobachtungsrichtung steht. Die kreisförmige Scheibe wird durch die Verkippung (Winkel i) zu einer Ellipse in der Projektionsebene. In der Projektionsebene nutzt man die Koordinaten X,Y zur Identifikation eines Punktes in der Ellipse.
Nun kommt der Spalt zum Modell hinzu: Der Spalt liegt in der Projektionsebene und überstreicht die Ellipse. Die Lage des Spaltes wird mit zwei Parametern beschrieben – zum einen mit dem Versatz b der Spaltlinie vom Zentrum (es ist der Abstand des Fußpunktes vom Zentrum) und zum anderen mit dem Winkel Theta, der den Winkel zwischen Spaltlinie und der X-Achse bezeichnet. Die Spaltkoordinate wird mit s beschrieben und mit ihr durchläuft man bei der späteren Berechnung die gesamte Spaltlänge.
Für einen Punkt (X,Y) ergibt sich die radiale Geschwindigkeitskomponente
Der Winkel Alpha liegt in der Scheibenebene und es besteht der Zusammenhang;
Mit diesen Modellannahmen kann man die durch den Spalt gemessene Geschwindigkeit wie folgt beschreiben:
Die Geschwindigkeit des Systems, also Bsp. die Fluchtgeschwindigkeit der Galaxie, in deren Zentrum die Gasscheibe liegt, ist Vsys, der zweite Term liefert die Geschwindigkeitsbeiträge, die der Spalt „aus“ der Projektionsellipse ausschneidet. Mit den Spaltparametern (b, Theta) kann man die Form der Geschwindigkeits-Modellkurve verändern. Die nachfolgende Grafik zeigt einen solchen Kurvenverlauf. Die X-Achse ist die Spaltkoordinate s, die Y-Achse zeigt die Radialgeschwindigkeiten – hier schon umgerechnet in Wellenlängen (Angstroem).
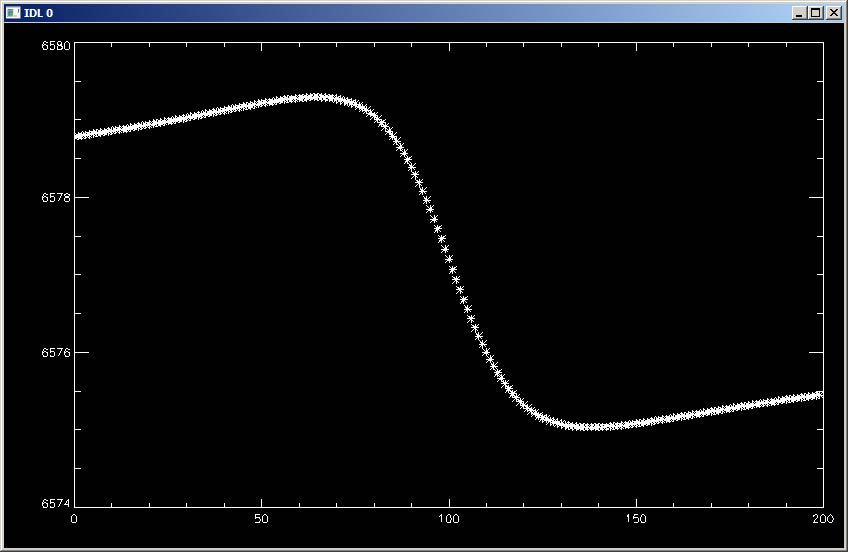
symmetrische Kurve der gemessenen Rotationsgeschwindigkeiten entlang des Spaltes. Das interessante bei dieser Modellbeschreibung ist der Umstand, das mit dem Versatz-Parameter b die Polstelle im Zentrum vermieden wird. Meist umgehen die Astronomen bei den galaktischen Rotationskurven dies, in dem sie den Zentrumsbereich ausklammern und dort eine starre Rotation ansetzen, die dann in eine Keplersche Scheibe übergeht.
Das Modell habe ich von F.Macchetto et al. übernommen, ihr findet den Fachartikel dazu unter … http://arxiv.org/abs/astro-ph/9706252. Dort gibt es auch weitere Bilder zur Erläuterung der Geometrie der Scheibenebene und der Projektionsebene.
Im folgenden werde ich dieses Modell benutzen, um damit die wellenförmige Variation der Ha-Linienlage zu beschreiben, die ich bei M 82 gemessen habe. Im Prinzip lässt es sich das Modell aber bei allen System anwenden, in denen man eine Scheibe vermutet, die aus Gas besteht, das um ein massives Zentrum rotiert.
Ich möchte Euch gerne die Modellfits an die M 82-SpaltA-Messwerte vorstellen.
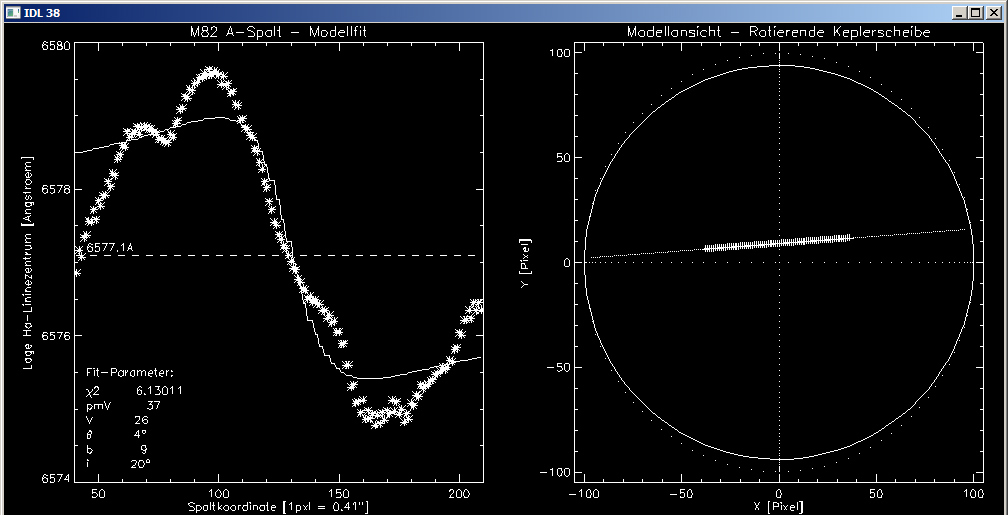
Die nachfolgenden Grafiken zeigen auf der linken Seite die Messwerte und die gefitteten Modellkurven. Die Fit-Parameter sind unten links aufgeführt. Auf der rechten Seite der Gasscheibe, die dem Modell zugrunde liegt dargestellt. Man erkennt gut, dass bei diesem Modell eine leichte Verkippung von ca. 20° ausreicht, um die gemessenen Wellenlänge, d.h. die Relativgeschwindigkeiten gut zu beschreiben.
In der Gasscheiben-Grafik ist die Lage der Spaltlinie mit Punkten skizziert, der benutzte Spaltausschnitt ist durch Pluszeichen als Plotsymbole hervorgehoben
Modell Fit 1 – Hier werden die Messungen bis zu den Maxima benutzt
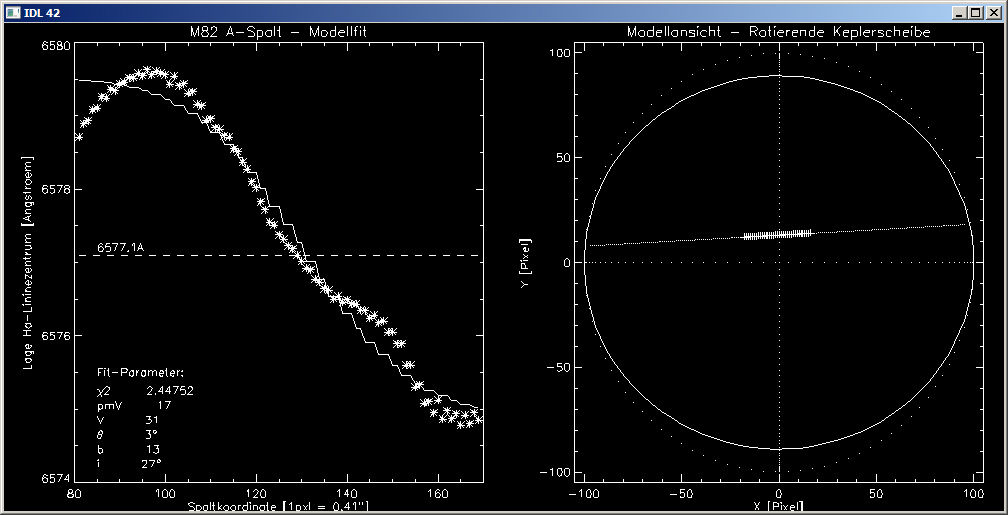
Modell Fit 2 – Es werden mehr Messwerte auf beiden Seiten hinzugenommen
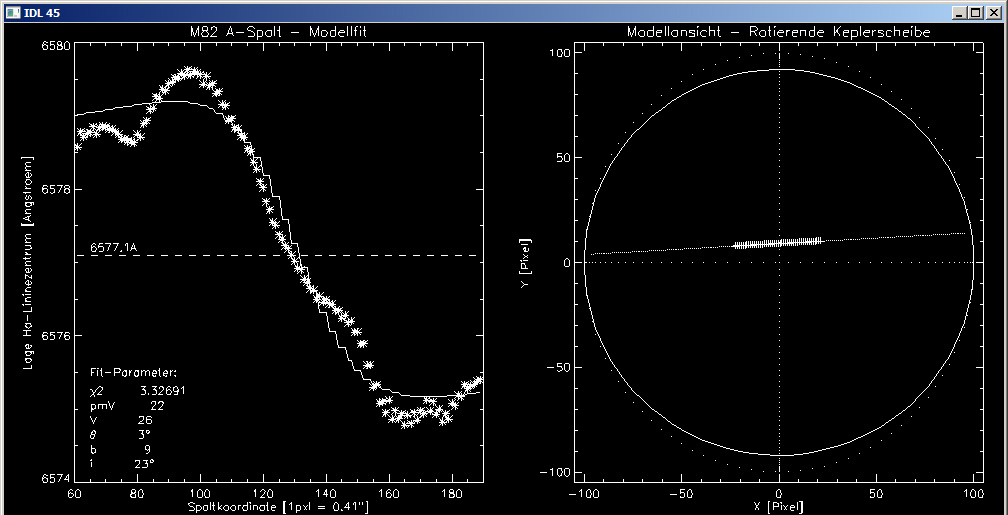
Modell Fit 3 – Die Messungen umfassen den gesamten Wellenverlauf
Die Ergebnisse der Modell-Fits lassen sich in folgender Form zusammenfassen:
- Der grundsätzliche Verlauf der Messwerte wird gut durch die Modellkurven beschrieben.
- Der äußere Abfall der Messwerte kann durch die Modellkurve prinzipiell erfasst werden, jedoch nicht deren Annäherung an die Nulllinie (6577.1A).
- Je mehr Messwerte aus den Randbereichen der Wellenfom hinzukommen, desto flacher ist die Gasscheibe geneigt, und desto geringer ist der Versatz b.
- Die Wellenform zeigt Variationen entlang der Modellkurve, auch nimmt die Qualität des Fits mit zunehmender Anzahl der Messwerte ab.
Was man beobachtet ist, dass das Modell nur in gewissen Grenzen die Realität in M 82 beschreibt. Gerade in den äußeren Bereichen stimmt die Annahme einer Keplerschen Gasscheibe nicht mehr, dies hängt auch damit zusammen, das dort die Amplitude der Ha-Linienzentren-Messungen deutlich zurückgeht.
Auch ist zu sagen, dass in diesem Modellbetrachtugnen die Intensität der Ha-Messungen noch keinen Einzug gefunden hat. Würde man dies tun, so müsste man ein Strahlungsmodell und damit ein Materiedichtemodell der Scheibe annehmen. Ein Teil dieser Betrachtung ist sicher auch ein Abschattungsmodell, da man annehmen kann, dass ein Teil der sichtbaren Wellenlängenvariation auch durch die Abschattung von Teilen der Scheibe zu erklären sein könnte.
Was sicher hilfreich wäre, aber das gilt wohl immer bei theoretischen Überlegungen, wären bessere Messwerte, d.h. eine bessere spektrale Auflösung der Wellenlängenmessungen. Ich würde annehmen, dass ich mit meinem Setup hier aber eine Grenze erreicht habe – mit meinem 300L/mm Gitter erreiche ich gute S/N Werte bei Einzelbelichtungen von 30min. Die Belichtungszeiten mit meinen höherauflösenden Gittern liegen außerhalb meiner Reichweite – eine Überlegung wäre die Nutzung einer schnelleren Optik. Vielleicht findet sich ja hier im Forum Mitstreiter in Sachen „Galaxienspektren mit niedriger Auflösung“.
Mit den oben beschriebenen Modell-Fits kann man nicht nur eine Hypothese bzgl. des inneren Aufbaus der Zentrums anstellen, sondern man kann auch die zentrale Masse abschätzen.
In der Modellbeschreibung steht vor dem Bruch ein Faktor, der neben der Gravitationskonstanten die zentrale Masse enthält:
Bei den Fits liegt dieser Wert bei 26A. Bezogen auf die Ha-Linienlage entspricht dies 1.19 × 10^6 m/s. Setzt man diesen Wert ein, so berechnet man für die zentrale Masse einen Wert von
M = 2,6 * 10^9 Sonnenmassen.
Aufgrund der enthaltenen Messfehler ist dieses Ergebnis mit Vorsicht zu genießen, aber die Größenordnung kann man als Masseninhalt innerhalb eines Bereich von ca. 2000–3000 Lichtjahren deuten. M 82 hat einen Durchmesser von ca. 40.000 Lichtjahren und ist damit deutlich kleiner als die Milchstrasse mit ihren 100.000 Lichtjahren Durchmesser. In der Literatur findet man für M 82 eine Gesamtmasse von 1.1 × 10^11 Sonnenmassen (http://arxiv.org/pdf/astro-ph/9803012.pdf). Die berechnete Zentralmasse entspräche dann etwa 2% der Gesamtmasse.
Bei diesen Überlegungen benutzt man nur die leuchtende Materie, die Dunkle Materie bleibt aussen vor. Dies relativiert sicher die Aussagekraft der Rechnung. Auch muss man bedenken, dass die berechnete Masse nicht die Masse des zentralen supermassiven Schwarzen Lochs ist, die berechnete „zentrale Masse“ kann man besser als Summe der zentralen Massen (SMBH, Akkretionsscheibe, Torus, innere Gasscheibe…) beschreiben.
Man findet einige Studien zu M 82, die mit verschiedenen Methoden die Massenverteilung zu beschreiben versuchen. U.a. findet man bei http://arxiv.org/abs/1012.1503 eine Angabe einer Masse von 10^10 innerhalb eines Bereichs von 6.400 Lichtjahren. Diese Angabe ist in guter Übereinstimmung mit dem Wert, der durch den Modellfit bestimmt wurde.
die Bestimmung der Fehler eines Modellfits erfolgt in der Regel über die Gewichtung der Messwerte. Man kann aber auch den Raum der Modellparameter ganz durchlaufen und das Schwanken der gefitteten Parameter verfolgen. Ich habe das für die Spalt-A-Modellfits einmal durchgeführt und dabei bin ich auch ein Chiquadrat-Minimum gestoßen, das einen etwas besseren Fit beschreibt:
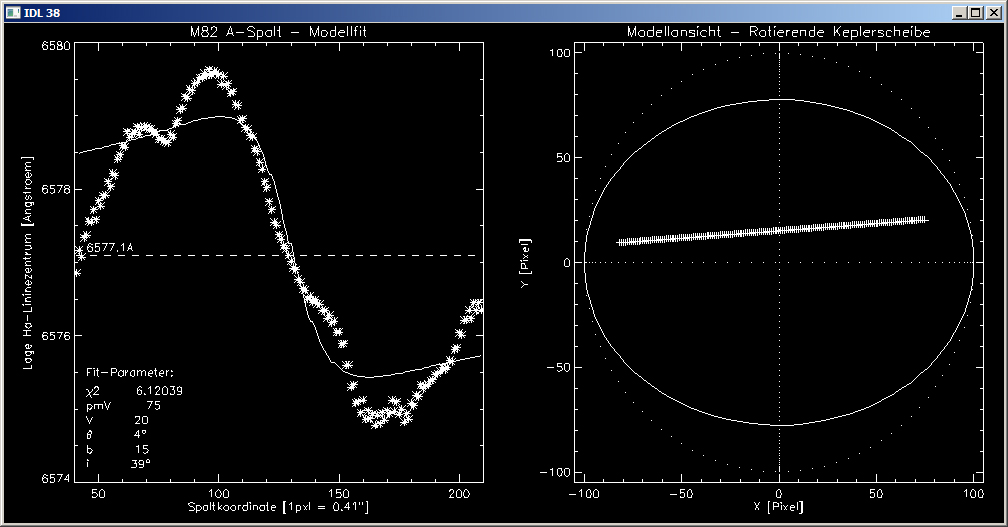
Der Vergleich dieser Werte mit dem obigen Fit, gibt eine Orientierung über die Fehlerbereiche – so ist die Genauigkeit der Inklination im Bereich von ±10°. Die Amplitude mit der Faktor, der die Zentralmasse enthält einen Fehler von ±5A. Mit dem besseren Fit ergibt sich eine Zentralmasse:
M = 1,5 × 10^9 Sonnenmassen
Führt man die gesamte Fit-Prozedur mit der gemessenen Werte der Spalt-B-Lage durch, so erhält man folgenden besten Fit:
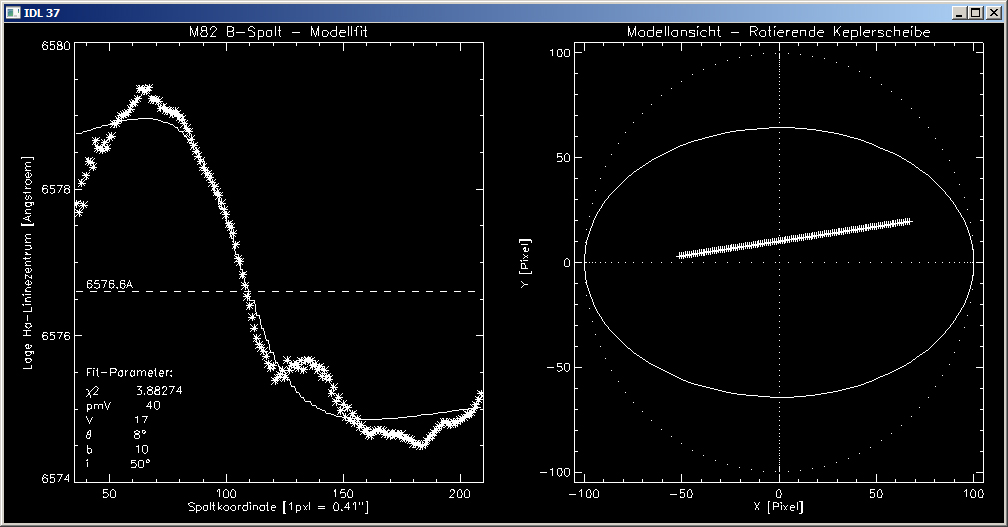
Die Daten der Spalt-B-Messung liegen, bedingt durch die Platzierung des Spaltes, nicht mehr symmetrisch zum Mittellinie. Diese liegt bei den Spalt-B Werte auch um 0.5A tiefer, dies ist aber auch die Ungenauigkeit der Eichung der beiden Spalt-Daten zurückzuführen. Hier interessieren v.a. die relativen Werte.
Man bestimmt mit den Spalt-B-Parametern die Zentralmasse zu:
M = 1,1 × 10^9 Sonnenmassen.
Die beiden anderen Spaltlagen C+D treffen nicht mehr diese „Scheibenregion“, dies kann man daher nicht für weitere Fits benutzen.
Abschließend kann ich sagen, dass mich verblüfft hat, mit welchen einfachen Spektroskopie-Methoden man Aussagen über die Astrophysik im Zentrum von M 82 treffen kann. Ich denke, dass dies bei anderen Galaxien schwerer wird, da M82 als helle Starburst-Galaxie mit der prominenten Ha-Linie die „Messsonde“ netterweise mitliefert.